Solving two-step equations is a fundamental skill in algebra, involving operations like multiplication, division, addition, and subtraction․ These equations require two steps to isolate the variable, making them slightly more complex than one-step equations․ Mastering this concept is crucial for progressing in math, as it builds problem-solving skills and logical thinking․ Worksheets and online tools provide ample practice opportunities, ensuring a thorough understanding of the process․ By breaking down problems into manageable steps, students can confidently tackle equations and apply these techniques to real-world scenarios․
What Are Two-Step Equations?
Two-step equations are algebraic expressions requiring two operations to solve for the variable․ They involve a combination of operations such as addition, subtraction, multiplication, or division․ For example, an equation like 3y + 6 = 12 requires first subtracting 6 and then dividing by 3 to find y․ These equations are fundamental in developing problem-solving skills, as they introduce the concept of performing inverse operations in the reverse order of operations․ Worksheets often include problems like (10/3)v + 25 = 50, reinforcing the methodical approach to solving them․
Why Are Two-Step Equations Important in Math?
Two-step equations are essential in math as they develop foundational algebraic skills, enabling students to solve for unknowns through systematic steps․ They prepare learners for more complex equations by reinforcing the order of operations and the use of inverse operations․ These equations enhance problem-solving abilities and logical thinking, crucial for advanced math and real-world applications․ Regular practice with worksheets improves accuracy and speed, ensuring a strong mathematical foundation for future challenges․
How to Approach Two-Step Equations
Approaching two-step equations involves systematically simplifying and isolating the variable․ First, identify and undo any operations on either side of the equation using inverse operations․ For example, subtract to undo addition or divide to undo multiplication․ Always apply operations to both sides to maintain balance․ Practice with worksheets helps build fluency, while checking solutions ensures accuracy․ By breaking problems into manageable steps and using algebraic properties, learners can confidently solve two-step equations and apply these strategies to more complex math challenges․

Understanding the Structure of Two-Step Equations
Two-step equations involve a variable and two operations, requiring two steps to solve․ They combine operations like multiplication, division, addition, or subtraction, structured to isolate the variable through inverse operations;
Identifying Operations in Two-Step Equations
In two-step equations, identifying operations is crucial․ Equations may involve multiplication or division combined with addition or subtraction․ For example, in 3y + 6 = 12, multiplication (3y) is followed by addition (+6)․ Similarly, 10 ⸺ 3v = 25 includes subtraction and multiplication․ Recognizing these operations helps in applying the correct inverse steps․ Worksheets often highlight such patterns, aiding students in systematically undoing operations to isolate variables․ This skill is foundational for solving more complex equations and ensures a clear path to finding variable values accurately․
The Role of Inverse Operations
In solving two-step equations, inverse operations play a vital role․ They help undo the operations applied to the variable, allowing it to be isolated․ For example, to solve 2x + 8 = 16, subtraction (inverse of addition) is first used to remove 8, resulting in 2x = 8․ Then, division (inverse of multiplication) isolates x, giving x = 4․ Worksheets emphasize the application of these inverses, ensuring students understand the systematic approach to simplifying equations and finding variable values effectively․
Common Mistakes in Structuring Equations
When structuring two-step equations, common mistakes include misapplying the order of operations and forgetting to reverse operations․ For instance, in 3(x + 4) = 21, some may incorrectly distribute multiplication before addition․ Others might fail to apply inverse operations properly, such as not dividing after subtracting․ Worksheets highlight these errors, guiding students to carefully follow each step and check their work․ Consistent practice helps minimize these mistakes, fostering a deeper understanding of equation structure and solution processes․
Step-by-Step Strategies for Solving Two-Step Equations
Start by simplifying both sides, then isolate the variable using inverse operations․ Verify your solution by substituting it back into the original equation to ensure accuracy․
Step 1: Simplify the Equation
Simplifying the equation is the first step in solving two-step equations․ This involves combining like terms, performing operations, and ensuring both sides of the equation are balanced․ Look for constants or variables that can be combined to reduce complexity․ For example, in the equation 3y + 6 = 12, subtract 6 from both sides to simplify it to 3y = 6․ This step makes the equation easier to work with and prepares it for isolating the variable; Always apply the same operation to both sides to maintain equality and accuracy․
Step 2: Isolate the Variable
After simplifying, the next step is to isolate the variable by performing inverse operations․ If the variable is multiplied or divided, use division or multiplication to solve for it․ For example, in 3y = 6, divide both sides by 3 to get y = 2․ If the equation involves addition or subtraction, reverse the operation to isolate the variable․ Always apply the same operation to both sides of the equation to maintain balance․ This step ensures the variable stands alone, allowing you to find its value accurately and efficiently․ Checking your solution by substituting it back into the original equation confirms its correctness․
Step 3: Check Your Solution
After isolating the variable, substitute your solution back into the original equation to verify its correctness․ This ensures both sides of the equation are equal, confirming your answer is accurate․ For example, if you solved for y in 3y + 6 = 12 and found y = 2, substituting y = 2 back into the equation results in 3(2) + 6 = 12, which simplifies to 12 = 12, validating your solution․ This step helps catch any mistakes made during the solving process and builds confidence in your math skills․ It’s a simple yet effective way to ensure accuracy and master two-step equations․

Practicing with Worksheets
Worksheets provide structured practice for mastering two-step equations, offering a variety of problems involving fractions, integers, and decimals․ Each worksheet typically includes 10-15 problems, ensuring thorough practice and skill mastery․ They often cover different operations, such as multiplication, division, addition, and subtraction, helping students gain confidence in solving equations․ Many worksheets are downloadable in PDF format, making them easily accessible for homework or self-study․ Regular practice with worksheets is essential for building problem-solving skills and understanding algebraic concepts․
Benefits of Using Worksheets for Practice
Worksheets offer structured practice, helping students master two-step equations through varied problems involving fractions, integers, and decimals․ They enhance problem-solving skills and logical thinking by providing clear examples and exercises․ Worksheets are ideal for homework or self-study, reinforcing classroom lessons and building confidence․ Their organized format allows for focused learning, ensuring students understand each step of solving equations․ Regular use of worksheets improves accuracy and speed, making them an essential tool for math education and skill development․
Types of Problems Found in Worksheets
Worksheets feature a variety of two-step equation problems, including those with integers, fractions, and decimals․ They cover operations like multiplication/division and addition/subtraction․ Some problems involve mixed operations, requiring students to apply multiple skills․ Word problems and real-world applications are also included to enhance understanding․ Worksheets may focus on specific challenges, such as negative coefficients or distributive properties, ensuring comprehensive practice․ This diversity helps students gain a deep understanding of equation-solving techniques and prepares them for more complex math concepts in the future․
Where to Find Reliable Worksheets
Reliable two-step equation worksheets can be found on educational websites like WorksheetWorks․com and Kuta Software․ These platforms offer a wide range of free and downloadable PDF resources, catering to various skill levels․ Many worksheets include problems involving integers, fractions, and decimals, as well as mixed operations․ Some also provide word problems and real-world applications; Additionally, websites like Teachers Pay Teachers and MathWorksheets4Kids offer high-quality, printable materials․ These resources are ideal for both classroom use and independent practice, ensuring students can master two-step equations effectively․

Handling Different Types of Two-Step Equations
Two-step equations involve operations like multiplication, division, addition, and subtraction․ They may include negative coefficients and mixed operations, requiring careful application of inverse operations and order of operations․
Solving Equations with Multiplication and Division
Solving two-step equations involving multiplication and division requires applying inverse operations․ Start by identifying the operations in the equation․ For example, in ( 3x = 12 ), divide both sides by 3 to isolate ( x )․ With negative coefficients, like ( -2x = 6 ), divide both sides by -2 to find ( x = -3 )․ For equations with both operations, such as ( 6x ÷ 3 = 12 ), simplify first by dividing 6 by 3 to get ( 2x = 12 ), then divide by 2․ Always check your solution by substituting back into the original equation to ensure accuracy․ Practice with various problems, including those involving fractions, integers, and decimals, to build proficiency․ Mastering these steps will enhance your algebraic problem-solving skills․
Solving Equations with Addition and Subtraction
Solving two-step equations involving addition and subtraction starts by isolating the term with the variable․ For example, in ( x + 4 = 10 ), subtract 4 from both sides to find ( x = 6 )․ With subtraction, like ( 8 ⸺ y = 3 ), subtract 8 and add y to both sides to get ( -y = -5 ), then multiply by -1 to solve for ( y = 5 )․ When dealing with negative numbers, ensure to apply inverse operations correctly; Practice with mixed equations involving fractions, integers, and decimals to refine your skills․ Always verify solutions by substituting back into the original equation to confirm accuracy․ This methodical approach ensures clarity and confidence in solving such equations․
Mixed Operations in Two-Step Equations
Mixed operations in two-step equations combine multiplication/division with addition/subtraction, requiring careful step-by-step execution․ For example, solve ( 3x + 6 = 24 ) by first subtracting 6 from both sides to isolate the term with the variable, resulting in ( 3x = 18 ), then dividing by 3 to find ( x = 6 )․ Similarly, in ( 8 — 2y = 4 ), isolate the variable by adding 2y and subtracting 4, leading to ( -2y = -4 ), and then dividing by -2 to get ( y = 2 )․ Always apply inverse operations in the correct order and verify solutions by substitution to ensure accuracy․ Practice with worksheets involving fractions, integers, and decimals to master these skills effectively․
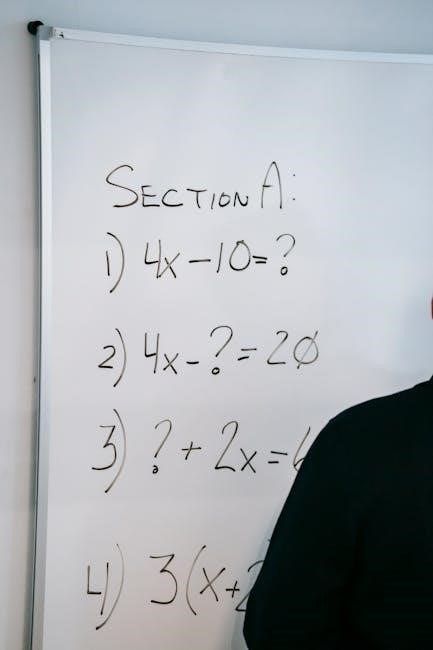
Advanced Techniques for Solving Two-Step Equations
Advanced techniques involve applying algebraic properties, such as the distributive property, to simplify complex equations․ These methods streamline solving processes, especially with negative coefficients or multi-step operations, enhancing problem-solving efficiency․
Using Algebraic Properties
Algebraic properties, such as the distributive property and inverse operations, are essential tools for solving two-step equations․ The distributive property allows you to simplify expressions like ( a(b + c) = ab + ac ), making it easier to isolate variables․ Additionally, understanding inverse operations helps undo additions or multiplications step-by-step․ For example, in the equation ( 3(x + 4) = 21 ), applying the distributive property first and then isolating ( x ) using inverse operations is key․ These properties not only simplify equations but also enhance problem-solving efficiency, as demonstrated in various worksheet exercises․
Working with Negative Coefficients
Negative coefficients in two-step equations require careful handling to maintain the equation’s balance․ When dividing or multiplying by a negative number, the inequality sign flips, ensuring the solution remains accurate․ For instance, in the equation ( -2x + 5 = 11 ), isolating ( x ) involves subtracting 5 and then dividing by -2, resulting in ( x = -3 )․ Worksheets often include such problems to practice handling negative coefficients, reinforcing the importance of sign management and proper application of inverse operations to avoid common errors in algebraic manipulation․
Applying Distributive Property
The distributive property is essential in simplifying two-step equations involving parentheses․ For example, in equations like 3(x + 4) = 21, distributing the 3 gives 3x + 12 = 21․ This step is crucial for isolating the variable․ Worksheets often include problems that require applying the distributive property before solving, ensuring students understand how to handle complex expressions․ Proper application of this property helps in breaking down equations systematically, making it easier to solve for the variable and verify the solution through substitution or graphing tools available online․

Common Challenges and Mistakes
Students often struggle with forgetting to reverse operations, misapplying the order of operations, and neglecting to simplify both sides of the equation, leading to incorrect solutions․
Forgetting to Reverse Operations
One common error is neglecting to reverse operations when isolating the variable․ For instance, if an equation involves multiplication, division is the inverse operation, not another multiplication․ Similarly, addition and subtraction must be reversed․ Worksheets often highlight this mistake, emphasizing the importance of undoing operations in the correct order․ Without this reversal, solutions remain incorrect, making it essential to emphasize this step during practice․ Properly applying inverse operations ensures variables are isolated correctly, leading to accurate solutions in two-step equations․ Consistent practice helps students avoid this pitfall and build confidence in their problem-solving abilities․
Misapplying the Order of Operations
Misapplying the order of operations is a frequent mistake when solving two-step equations․ Many students fail to prioritize operations correctly, leading to incorrect solutions․ For example, in an equation like 3x + 6 = 24, some may add before multiplying, which disrupts the equation’s balance․ Worksheets often include reminders to follow PEMDAS (Parentheses, Exponents, Multiplication/Division, Addition/Subtraction)․ Ignoring this sequence can result in errors, such as dividing before undoing addition․ Practicing with worksheets helps reinforce the proper order, ensuring accurate solutions and a stronger grasp of algebraic principles․
Neglecting to Simplify Both Sides
Neglecting to simplify both sides of an equation is a common error when solving two-step equations․ Students often forget to combine like terms or simplify expressions on one or both sides, leading to incorrect solutions․ For example, in an equation like 3x + 6 = 24, failing to simplify before isolating the variable can result in errors․ Worksheets emphasize the importance of simplifying both sides first to maintain balance․ This step ensures accuracy and prevents mistakes․ Regular practice with worksheets helps students develop the habit of simplifying thoroughly before proceeding to isolate the variable․

Real-World Applications of Two-Step Equations
Two-step equations are essential in everyday scenarios, such as budgeting, cooking, and science․ They help solve problems like splitting bills, calculating speeds, and adjusting recipes, making math practical and relevant․
Everyday Scenarios Involving Two-Step Equations
Two-step equations are frequently used in daily life, such as calculating budgets, adjusting recipes, and determining distances․ For example, splitting a bill equally among friends or scaling a recipe requires solving two-step equations․ Similarly, calculating the time needed to travel a certain distance at a specific speed involves these equations․ They also apply to shopping discounts and combining quantities, making math practical and essential for problem-solving in real-world situations․ Such scenarios emphasize the importance of mastering two-step equations for everyday decision-making and efficiency․ Worksheets often include these real-life examples to enhance understanding and application․
Science and Engineering Applications
Two-step equations are integral to science and engineering, where they model real-world phenomena․ In physics, equations involving velocity, acceleration, and time often require two-step solutions․ Engineers use these equations to calculate stress on materials or fluid flow rates․ Chemistry problems, such as determining concentrations or reaction rates, also rely on two-step equations․ They are essential for designing experiments, optimizing systems, and ensuring safety in construction and manufacturing․ Worksheets and practice problems help students and professionals alike apply mathematical concepts to solve complex scientific and engineering challenges effectively and accurately․ This practical application underscores their importance in technical fields․
Financial and Budgeting Examples
Two-step equations are invaluable in financial planning and budgeting․ For instance, calculating total expenses involving taxes or discounts requires solving equations like ( 1․2x + 50 = 150 ), where ( x ) represents the original price․ Budget allocations, such as distributing funds across categories, also use two-step equations to ensure accurate distribution․ Additionally, determining savings goals or investment returns often involves solving equations with multiple operations, making them practical tools for personal finance and professional budgeting․ Worksheets provide realistic financial scenarios to hone these essential skills effectively․

Using Technology to Solve Two-Step Equations
Graphing calculators and online tools simplify solving two-step equations by providing step-by-step solutions․ Math software, like Kuta and WorksheetWorks, offers digital worksheets for practice and verification of answers․
Graphing Calculators and Solving Equations
Graphing calculators are powerful tools for solving two-step equations, offering step-by-step solutions and graphical representations․ They simplify complex problems, verify answers, and provide visual insights․ Many worksheets, like those from Kuta Software and WorksheetWorks, complement calculator use by offering digital practice․ These tools enhance understanding, reduce errors, and save time, making them invaluable for students mastering algebra․ By integrating technology with traditional methods, learners can deepen their problem-solving skills and confidently tackle equations․
Online Tools for Checking Solutions
Online tools are invaluable for verifying solutions to two-step equations․ Websites like Kuta Software and WorksheetWorks offer digital worksheets that allow students to input their answers and receive immediate feedback․ These platforms often provide step-by-step solutions, helping learners understand where they might have gone wrong․ Additionally, some tools offer interactive exercises that simulate solving equations, reinforcing the concepts learned through traditional practice․ By leveraging these resources, students can ensure the accuracy of their solutions and build confidence in their problem-solving abilities․
Math Software for Practice
Math software like Kuta Software and WorksheetWorks offers comprehensive tools for practicing two-step equations․ These programs provide customizable worksheets, allowing users to focus on specific operations or mixed problems․ They often include features for generating problems with fractions, integers, and decimals․ Many software solutions also offer interactive exercises where students can input their answers and receive immediate feedback․ This technology enhances learning by providing a dynamic and engaging environment, helping students master two-step equations through repeated practice and review․ These tools are ideal for both classroom and independent study settings․
Word Problems Involving Two-Step Equations
Word problems involving two-step equations require translating real-life scenarios into algebraic expressions․ These problems often involve age, distance, and financial calculations, enhancing problem-solving skills and logical thinking․
Translating Words into Algebraic Expressions
Translating words into algebraic expressions is a critical step in solving word problems involving two-step equations․ This process requires identifying key terms, assigning variables, and interpreting phrases like “is,” “more than,” or “less than․” For example, in problems involving age or distance, understanding how to convert descriptive language into mathematical operations is essential․ Worksheets often include scenarios like Ronald being x years old and his friend Colin being 3 years older, which translates to equations like x + 3․ By breaking down complex sentences into simpler parts, students can accurately form equations and solve them systematically․
Solving Age-Related Problems
Solving age-related problems involves translating real-world scenarios into algebraic equations․ For example, if Ronald is x years old and his friend Colin is 3 years older, the equation becomes x + 3․ Worksheets often include such problems, requiring students to set up and solve two-step equations․ By identifying key terms like “is” and “older than,” learners can form equations and apply inverse operations to find the unknown age; These problems enhance understanding of algebraic relationships and practical application of two-step equations in everyday life, making math more relatable and engaging for students․
Distance and Speed Problems
Distance and speed problems often involve two-step equations, where students must account for both rate and time․ For example, if a car travels 120 miles at 40 mph, the equation might be 120 = 40t + 20, where t is time in hours․ Solving such problems requires setting up the equation, isolating the variable through inverse operations, and interpreting the result․ Worksheets provide numerous scenarios, such as finding speed or distance, to practice these skills․ These problems bridge algebra with real-world applications, enhancing problem-solving abilities and practical understanding of mathematical concepts․

Assessing Understanding and Mastery
Quizzes, tests, and peer reviews help evaluate mastery of two-step equations․ Self-assessment techniques allow students to track progress and identify areas needing improvement for better retention and fluency․
Quizzes and Tests
Quizzes and tests are essential tools for assessing student understanding of two-step equations․ They provide a structured way to evaluate problem-solving skills and identify areas where additional practice is needed․ Worksheets and online tools offer a variety of test questions, such as solving for variables in equations like 3y + 6 = 12 or 10 — 3v = 25․ These assessments help teachers track progress and ensure students can apply inverse operations and algebraic properties correctly․ Regular testing also builds confidence and fluency in solving equations․
Peer Review and Collaboration
Peer review and collaboration are valuable strategies for mastering two-step equations․ Students can exchange worksheets, review each other’s solutions, and discuss problem-solving methods․ This approach fosters a deeper understanding by allowing learners to explain their thought processes and learn from one another․ Collaborative activities, such as solving equations like 6a + 4 = 2 or 9x, 7 = 7, encourage teamwork and communication․ It also helps identify common mistakes and reinforces proper techniques, creating a supportive learning environment that enhances problem-solving skills and confidence․
Self-Assessment Techniques
Self-assessment is a powerful tool for improving skills in solving two-step equations․ After completing worksheets, students should review their work to identify errors and understand where they went wrong․ Techniques include checking each step for accuracy, ensuring operations are reversed correctly, and verifying solutions by substituting them back into the original equation․ For example, solving 3y + 6 = 12 involves isolating y by subtracting 6 and then dividing by 3․ Regular self-assessment builds confidence, reinforces correct methods, and helps students master problem-solving independently;
Mastery of two-step equations comes through consistent practice and review․ Worksheets provide structured exercises to refine skills, ensuring confidence in solving real-world problems effectively and accurately․
Solving two-step equations involves isolating the variable through inverse operations․ Start by simplifying both sides, then undo addition or subtraction, followed by multiplication or division․ Practice worksheets help refine skills, covering integers, decimals, and fractions․ Mastering these equations builds foundational algebra skills, essential for advanced math and real-world applications․ Regular practice and reviewing common mistakes ensure confidence and accuracy in solving two-step problems effectively․
Encouragement for Continued Practice
Consistent practice is key to mastering two-step equations․ As you work through worksheets, remember that each problem solved is a step toward building strong algebraic skills․ Celebrate small victories and don’t hesitate to use online tools for support․ Embrace challenges as opportunities to grow, and stay motivated by tracking your progress․ With persistence and dedication, you’ll become confident in solving two-step equations and be well-prepared for more complex math concepts ahead․
Final Tips for Mastery
To achieve mastery in solving two-step equations, always approach each problem methodically․ First, simplify the equation by performing operations like combining constants or coefficients․ Next, use inverse operations to isolate the variable․ Check your solution by substituting it back into the original equation․ Regular practice with worksheets helps reinforce these steps․ Utilize online tools to verify answers and gain additional practice․ By staying organized and patient, you’ll develop a strong foundation in solving two-step equations and build confidence for more challenging algebraic problems ahead․
